在以前的幾篇文章中,我們討論了幾個運營分析中的案例。其中之一就有呼叫中心的訪客分配算法,今天的案例有些相似,但不再是個別的訪客分配而是討論更廣泛的內容。我們將使用一個與運籌學中的運輸算法來解決呼入分配最優化問題。
案例研究
你擁有一個含1000個資源(席位)的呼叫中心,每個席位都經過了一系列的培訓。培訓分為ABCDEF系列。例如,A類坐席是指已通過1~6號課程培訓的客服人數,而B類客服則通過了其它系列課程。各類坐席的分布如下
A : 200
B : 200
C : 100
D : 100
E : 250
F : 150
另外,每天呼入的電話有不同的問詢類型,大致可以分為4類。我們暫稱之為X、Y、Z和W類問詢。問詢的類型可以通過IVR(互動式語音應答系統)識別出來,你可以任意指定為這些客戶服務的坐席。工作日呼入問詢類型的大致分布為:
X : 20%
Y : 30%
Z : 15%
W : 35%
各工作日的呼入類型數量可能有差別,但各類問詢電話的占比基本是不變的。經過相應問詢類型的應答培訓,客服就可以獲得快速解答問詢的技巧。例如,經過A類培訓的客服可以在10分鐘內解答X類問詢。以下表格給出了經過某類培訓的客服應答某類問詢所需的相應時間。
表1 時間成本矩陣
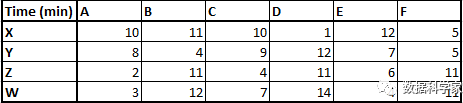
任務來了,你的建模目標就是讓呼叫中心各坐席的總應答時間最少。你可以讓坐席經過不同類型的培訓獲得問詢解答技巧,通過實時監督來減少應答的時間。但最終,你需要的是一個能做實時呼入分配的自動化系統,以實現所有席位被占用的總應答時間最小。
為簡單起見,我們把實際的呼入數假設為幾個確定的值。某呼叫中心每天呼入的各類問詢分布如下:
X : 200 個呼入
Y : 300個呼入
Z : 150個呼入
W : 350個呼入
總呼入數 : 1000
這時,客服的數量與呼入的數量是完全相等的。即使呼入的總數會增加,只要呼入問詢的類型保持著穩定的比率,我們后面要討論的解決方案仍然是有效。
運輸問題介紹
可以把呼入響應優化問題用運輸問題模型來解決,解答問詢的時間可以看成是運輸問題中的運輸成本。運輸問題是經典的線性規劃問題,其典型提法是:為了把某種產品從若干個產地調運到若干個銷地,已知每個產地的供應量和每個銷地的需求量,如何在許多可行的調運方案中,確定一個總運輸費或總運輸量最少的方案。運輸問題的解法有單純形法和表上作業法,運輸問題的一般解決方案有兩個步驟:
1. 制訂基本可行方案;
2. 找出最優方案。
運輸問題的基本可行方案可通過三種方法獲得:
1. 西北角法(最簡單的方法)
2. 最小成本法
3. 罰金成本法(伏格爾法)
西北角法
過程很簡單,每一次都在表格的西北角(左上角)放上最大的可能值,然后劃掉已滿足最大值要求的行或列,再對剩下的表格重復這一操作即可。比如在下表的左上角應該先填上200這個坐席數,然后劃掉X行和A列。
表2 西北角法初始運算
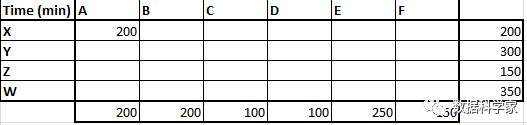
之所以填200,是因為x類呼入最多有200個,經過A類培訓的坐席也有200個,因此200是最大的可能值。劃掉X行和A列后,表的左上角變成了Y行B列,在這單元格的列向上要求有200個坐席經過B類培訓,行向上要求能應答300個Y類問題的呼入,因此這一單元格可以填入的最大可能值只能為200。這時列向上的坐席數滿足了,行向上還差300-200=100個坐席,所以只能把B列劃掉而要保留Y行。當下一個左上角變為Y行D列時,我們很容易可以判斷出這一單元格應該填入100。以此類推,可以找出所有可靠的坐席分配數。
表3 西北角法運算結果
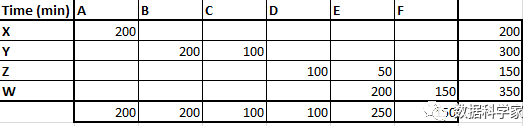
根據上表的計算結果和表1成本矩陣,我們可以計算出總的應答時長:200×10+200×4+100×9+100×11+50×6+200×4+150×11=7550分鐘。按照這一計算結果,我們可以將分配方案定為:讓所有受過A類培訓的客服應答X類問詢;將33%的Y類問詢分配給受過C類培訓的客服, 66%的Y類問詢分配給受過B類培訓的客服……。顯然,這一方案并不是最優的,以下兩種方法可以獲得更少的時間消耗。
最小成本法
最小成本法是另一種有所改進的運輸問題算法。在解決坐席-客戶匹配問題時我們先找出平均應答時間最少的。比如在本案例中,通過觀察表1的成本矩陣,我們發現X類客戶與D類坐席匹配耗時最少。所以我們先把最大可能的資源數匹配給這對組合。由于X類客戶平均有200位,而D類坐席最多只有100位,因此匹配給這對組合的最大可能資源數為100。
表4 最小成本法初始運算
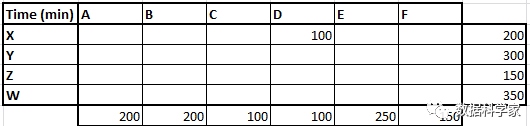
以此類推,我們依次找出余下成本單元格中的最小值,并將相應的最大可能資源數匹配到那些單元格中去,直到所有資源分配完畢。分配結果如下表所示:
表5 西北角法運算結果
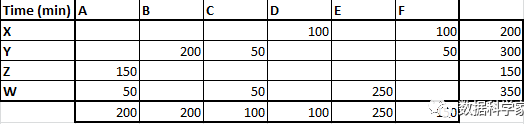
總的時間成本為:100×1+100×5+200×4+50×9+50×5+150×2+50×3+50×7+250×4=3900分鐘,與西北角法相比,總耗時減少了將近50%。
罰金成本法
這也是一種對初始分配過程有更多改進的算法。首先,我們計算每一行、每一列上最小成本和次小成本的差值,這一差值意味著如果我們沒有選出最小值而會遭受的成本損失,罰金成本法也因此得名(也稱伏格爾法)。其確定初始基本可行解的思路是:罰金成本最高的行或列中成本最低者優先考慮。以下為將成本矩陣轉化后的罰金成本表(最右側增加了各行罰金列,最下端增加了各列罰金行)。
表6罰金成本法初始運算
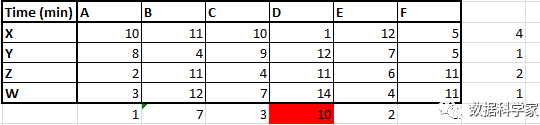
我們發現最大罰金出現在D列,我們應該馬上把該列最大的資源數分配給這列中的最小成本單元格。接下來,在余下的表格中我們再依次定位罰金最大成本行/列,及其最小的單元格,并進行相應資源數的分配(原則依然是不能超過行或列上的資源數限制)。完成分配后的結果如下表所示:
表7 罰金成本法運算結果
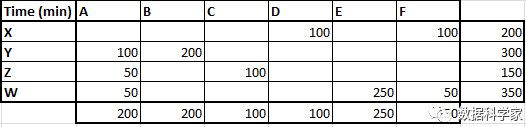
累計可得,總的時間成本為4400。可見,這種改進方法并不比最小成本法耗時少。這是因為恰好在這個案例中,最小成本法的迭代過程中并沒有出現因未選最低成本而使總成本懲罰性增加的情形。
找出最優解
通過上述算法的計算,可以基本斷定最小成本法就是我們要找的最優解。但在解決更一般的成本優化問題時,往往需要引入進一步的討論:最優解的判別與解的改進。本例中我們不再深入介紹這一過程,留待讀者自行學習。可以提示的是:解的最優性檢驗包含閉回路法和位勢法;而從一個方案調整到最優方案的過程,就是單純形法的過程。
“運輸問題”在運籌學方面應用很廣,但在數據分析領域應用不多。通過本例,我們可以看到將呼叫響應優化問題轉化為運輸問題解決時,所帶來的顯著的成本優化。

































































































 京公網安備 11010502049343號
京公網安備 11010502049343號