精品国产一级在线观看,国产成人综合久久精品亚洲,免费一级欧美大片在线观看

在理解大數據方面，聚類是一種很常用的基本方法。近日，數據科學家兼程序員 Peter Gleeson 在 freeCodeCamp 發布了一篇深度講解文章，對一些聚類算法進行了基礎介紹，并通過簡單而詳細的例證對其工作過程進行了解釋說明。

看看下面這張圖，有各種各樣的蟲子和蝸牛，你試試將它們分成不同的組別?

不是很難吧，先從找出其中的蜘蛛開始吧!

完成了嗎?盡管這里并不一定有所謂的「正確答案」，但一般來說我們可以將這些蟲子分成四組：蜘蛛、蝸牛、蝴蝶/飛蛾、蜜蜂/黃蜂。

很簡單吧?即使蟲子數量再多一倍你也能把它們分清楚，對嗎?你只需要一點時間以及對昆蟲學的熱情就夠了——其實就算有成千上萬只蟲子你也能將它們分開。

但對于一臺機器而言，將這 10 個對象分類成幾個有意義的分組卻并不簡單——在一門叫做組合學(combinatorics)的數學分支的幫助下，我們知道對于這 10 只蟲子，我們可以有 115,975 種不同的分組方式。如果蟲子數量增加到 20，那它們可能的分組方法將超過 50 萬億種。要是蟲子數量達到 100，那可能的方案數量將超過已知宇宙中的粒子的數量。超過多少呢?據我計算，大約多 500,000,000,000,000,000,000,000,000,000,000,000 倍，已是難以想象的超天文數字!

但其中大多數分組方案都是無意義的，在那些浩如煙海的分組選擇中，你只能找到少量有用的蟲子分組的方法。

而我們人類可以做得很快，我們往往會把自己快速分組和理解大量數據的能力看作是理所當然。不管那是一段文本，還是屏幕上圖像，或是對象序列，人類通常都能有效地理解自己所面對的數據。

鑒于人工智能和機器學習的關鍵就是快速理解大量輸入數據，那在開發這些技術方面有什么捷徑呢?在本文中，你將閱讀到三種聚類算法——機器可以用其來快速理解大型數據集。當然，除此之外還有其它的算法，但希望這里的介紹能給你一個良好的開始!

在本文中，我將給出每種聚類算法的概述、工作方式的簡單介紹和一個更細節的逐步實現的案例。我相信這能幫助你理解這些算法。

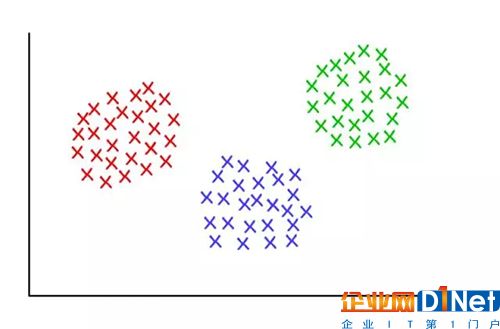
3 個齊整的聚類，K=3

一、K-均值聚類(K-means clustering)

1. 何時使用?

當你事先知道你將找到多少個分組的時候?

2. 工作方式

該算法可以隨機將每個觀察(observation)分配到 k 類中的一類，然后計算每個類的平均。接下來，它重新將每個觀察分配到與其最接近的均值的類別，然后再重新計算其均值。這一步不斷重復，直到不再需要新的分配為止。

3. 有效案例

假設有一組 9 位足球運動員，他們中每個人都在這一賽季進了一定數量的球(假設在 3-30 之間)。然后我們要將他們分成幾組——比如 3 組。

第一步：需要我們將這些運動員隨機分成 3 組并計算每一組的均值。

第 1 組

第 2 組

第 3 組

第二步：對于每一位運動員，將他們重新分配到與他們的分數最接近的均值的那一組;比如，運動員 A(5 個球)被重新分配到第 2 組(均值=11)。然后再計算新的均值。

第 1 組(原來的均值=12)

第 2 組(原來的均值=11)

第 3 組(原來的均值=16)

不斷重復第二步，直到每一組的均值不再變化。對于這個簡單的任務，下一次迭代就能達到我們的目標。現在就完成了，你已經從原數據集得到了 3 個聚類!

第 1 組(原來的均值=10)

第 2 組(原來的均值=4.33)

第 3 組(原來的均值=21)

通過這個例子，該聚類可能能夠對應這些運動員在球場上的位置——比如防守、中場和進攻。K-均值在這里有效，是因為我們可以合理地預測這些數據會自然地落到這三個分組中。

以這種方式，當給定一系列表現統計的數據時，機器就能很好地估計任何足球隊的隊員的位置——可用于體育分析，也能用于任何將數據集分類為預定義分組的其它目的的分類任務。

4. 更加細微的細節：

上面所描述的算法還有一些變體。最初的「種子」聚類可以通過多種方式完成。這里，我們隨機將每位運動員分成了一組，然后計算該組的均值。這會導致最初的均值可能會彼此接近，這會增加后面的步驟。

另一種選擇種子聚類的方法是每組僅一位運動員，然后開始將其他運動員分配到與其最接近的組。這樣返回的聚類是更敏感的初始種子，從而減少了高度變化的數據集中的重復性。但是，這種方法有可能減少完成該算法所需的迭代次數，因為這些分組實現收斂的時間會變得更少。

K-均值聚類的一個明顯限制是你必須事先提供預期聚類數量的假設。目前也存在一些用于評估特定聚類的擬合的方法。比如說，聚類內平方和(Within-Cluster Sum-of-Squares)可以測量每個聚類內的方差。聚類越好，整體 WCSS 就越低。

二、層次聚類(Hierarchical clustering)

1. 何時使用?

當我們希望進一步挖掘觀測數據的潛在關系，可以使用層次聚類算法。

2. 工作方式

首先我們會計算距離矩陣(distance matrix)，其中矩陣的元素(i，j)代表觀測值 i 和 j 之間的距離度量。然后將最接近的兩個觀察值組為一對，并計算它們的平均值。通過將成對觀察值合并成一個對象，我們生成一個新的距離矩陣。具體合并的過程即計算每一對最近觀察值的均值，并填入新距離矩陣，直到所有觀測值都已合并。

3. 有效案例：

以下是關于鯨魚或海豚物種分類的超簡單數據集。作為受過專業教育的生物學家，我可以保證通常我們會使用更加詳盡的數據集構建系統。現在我們可以看看這六個物種的典型體長。本案例中我們將使用 2 次重復步驟。

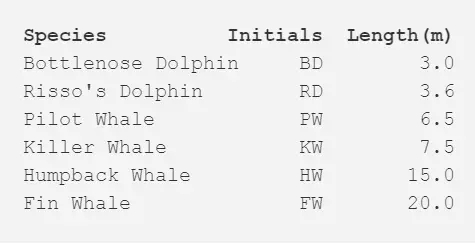
步驟一：計算每個物種之間的距離矩陣，在本案例中使用的是歐氏距離(Euclidean distance)，即數據點(data point)間的距離。你可以像在道路地圖上查看距離圖一樣計算出距離。我們可以通過查看相關行和列的交叉點值來查閱任一兩物種間的長度差。

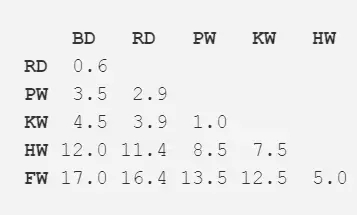
步驟二：將兩個距離最近的物種挑選出來，在本案例中是寬吻海豚和灰海豚，他們平均體長達到了 3.3m。重復第一步，并再一次計算距離矩陣，但這一次將寬吻海豚和灰海豚的數據使用其均值長度 3.3m 代替。

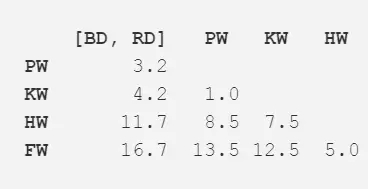
接下來，使用新的距離矩陣重復步驟二。現在，最近的距離成了領航鯨與逆戟鯨，所以我們計算其平均長度(7.0m)，并合并成新的一項。

隨后我們再重復步驟一，再一次計算距離矩陣，只不過現在將領航鯨與逆戟鯨合并成一項且設定長度為 7.0m。

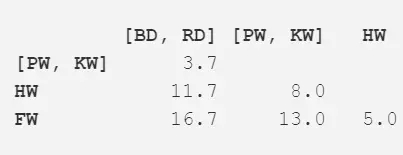
我們再一次使用現在的距離矩陣重復步驟 2。最近的距離(3.7m)出現在兩個已經合并的項，現在我們將這兩項合并成為更大的一項(均值為 5.2m)。

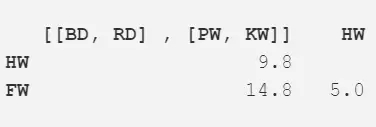
緊接著，我們再一次重復步驟 2，最小距離(5.0m)出現在座頭鯨與長須鯨中，所以繼續合并它們為一項，并計算均值(17.5m)。

返回到步驟 1，計算新的距離矩陣，其中座頭鯨與長須鯨已經合并為一項。

最后，重復步驟 2，距離矩陣中只存在一個值(12.3m)，我們將所有的都合成為了一項，并且現在可以停止這一循環過程。先讓我們看看最后的合并項。

現在其有一個嵌套結構(參考 JSON)，該嵌套結構能繪制成一個樹狀圖。其和家族系譜圖的讀取方式相近。在樹型圖中，兩個觀察值越近，它們就越相似和密切相關。

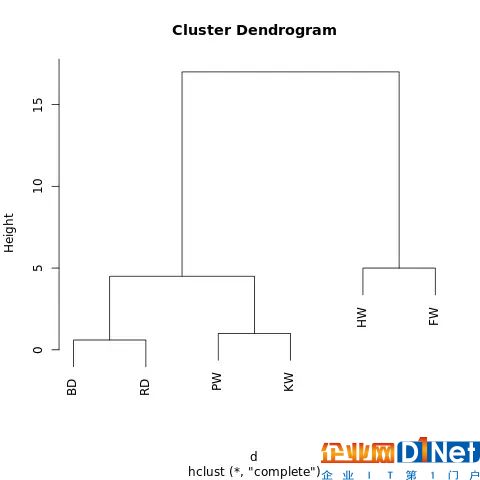
一個在 R-Fiddle.org 生成的樹狀圖

通過樹型圖的結構，我們能更深入了解數據集的結構。在上面的案例中，我們看到了兩個主要的分支，一個分支是 HW 和 FW，另一個是 BD、RD、PW、KW。

在生物進化學中，通常會使用包含更多物種和測量的大型數據集推斷這些物種之間的分類學關系。在生物學之外，層次聚類也在機器學習和數據挖掘中使用。

重要的是，使用這種方法并不需要像 K-均值聚類那樣設定分組的數量。你可以通過給定高度「切割」樹型以返回分割成的集群。高度的選擇可以通過幾種方式進行，其取決于我們希望對數據進行聚類的分辨率。

例如上圖，如果我們在高度等于 10 的地方畫一條線，就將兩個主分支切開分為兩個子圖。如果我們從高度等于 2 的地方分割，就會生成三個聚類。

4. 更多細節：

對于這里給出的層次聚類算法(hierarchical clustering algorithms)，其有三個不同的方面。

最根本的方法就是我們所使用的集聚(agglomerative)過程，通過該過程，我們從單個數據點開始迭代，將數據點聚合到一起，直到成為一個大型的聚類。另外一種(更高計算量)的方法從巨型聚類開始，然后將數據分解為更小的聚類，直到獨立數據點。

還有一些可以計算距離矩陣的方法，對于很多情況下，歐幾里德距離(參考畢達哥拉斯定理)就已經夠了，但還有一些可選方案在特殊的情境中更加適用。

最后，連接標準(linkage criterion)也可以改變。聚類根據它們不同的距離而連接，但是我們定義「近距離」的方式是很靈活的。在上面的案例中，我們通過測量每一聚類平均值(即形心(centroid))之間的距離，并與最近的聚類進行配對。但你也許會想用其他定義。

例如，每個聚類有幾個離散點組成。我們可以將兩個聚類間的距離定義為任意點間的最小(或最大)距離，就如下圖所示。還有其他方法定義連接標準，它們可能適應于不同的情景。

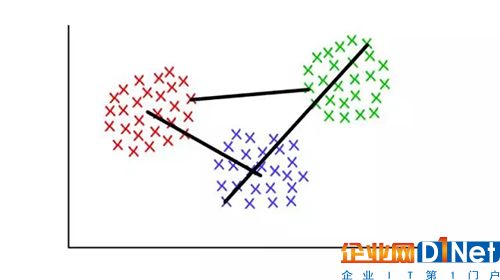
紅/藍：形心連接;紅/綠：最小連接;綠/藍：最大連接

三、圖團體檢測(Graph Community Detection)

1. 何時使用?

當你的數據可以被表示為一個網絡或圖(graph)時。

2. 工作方式

圖團體(graph community)通常被定義為一種頂點(vertice)的子集，其中的頂點相對于網絡的其它部分要連接得更加緊密。存在多種用于識別圖的算法，基于更具體的定義，其中包括(但不限于)：Edge Betweenness、Modularity-Maximsation、Walktrap、Clique Percolation、Leading Eigenvector……

3. 有效案例

圖論是一個研究網絡的數學分支，參考機器之心文章《想了解概率圖模型?你要先理解圖論的基本定義與形式》。使用圖論的方法，我們可以將復雜系統建模成為「頂點(vertice)」和「邊(edge)」的抽象集合。

也許最直觀的案例就是社交網絡。其中的頂點表示人，連接頂點的邊表示他們是朋友或互粉的用戶。

但是，要將一個系統建模成一個網絡，你必須要找到一種有效連接各個不同組件的方式。將圖論用于聚類的一些創新應用包括：對圖像數據的特征提取、分析基因調控網絡(gene regulatory networks)。

下面給出了一個入門級的例子，這是一個簡單直接的圖，展示了我最近瀏覽過的 8 個網站，根據他們的維基百科頁面中的鏈接進行了連接。這個數據很簡單，你可以人工繪制，但對于更大規模的項目，更快的方式是編寫 Python 腳本。這里是我寫的一個：

https://raw.githubusercontent.com/pg0408/Medium-articles/master/graph_maker.py

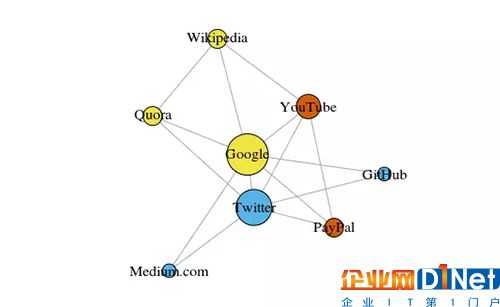
用 R 語言 3.3.3 版中的 igraph 繪制的圖

這些頂點的顏色表示了它們的團體關系，大小是根據它們的中心度(centrality)確定的。可以看到谷歌和 Twitter 是最中心的吧?

另外，這些聚類在現實生活中也很有意義(一直是一個重要的表現指標)。黃色頂點通常是參考/搜索網站，藍色頂點全部是在線發布網站(文章、微博或代碼)，而橙色頂點是 YouTube 和 PayPal——因為 YouTube 是由前 PayPal 員工創立的。機器還算總結得不錯!

除了用作一種有用的可視化大系統的方式，網絡的真正力量是它們的數學分析能力。讓我們將上面圖片中的網絡翻譯成更數學的形式吧。下面是該網絡的鄰接矩陣(adjacency matrix)：

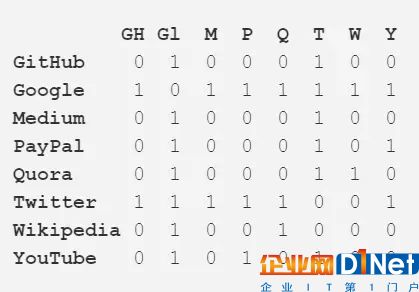
每行和每列的交點處的值表示對應的頂點對之間是否存在邊。比如說，在 Medium 和 Twitter 之間有一條邊，所以它們的行列交點是 1。類似地，Medium 和 PayPal 之間沒有邊，所以它們的行列交點是 0.

該鄰接矩陣編碼了該網絡的所有屬性——其給了我們開啟所有有價值的見解的可能性的鑰匙。首先，每一行或每一列的數字相加都能給你關于每個頂點的程度(degree)——即它連接到了多少個其它頂點，這個數字通常用字母 k 表示。類似地，將每個頂點的 degree 除以 2，則能得到邊的數量，也稱為鏈接(link)，用 L 表示。行/列的數量即是該網絡中頂點的數量，稱為節點(node)，用 N 表示。

只需要知道 k、L 和 N 以及該鄰接矩陣 A 中每個單元的值，就能讓我們計算出該網絡的任何給定聚類的模塊性(modularity)。

假設我們已經將該網絡聚類成了一些團體。我們就可以使用該模塊性分數來評估這個聚類的質量。分數更高表示我們將該網絡分割成了「準確的(accurate)」團體，而低分則表示我們的聚類更接近隨機。如下圖所示：

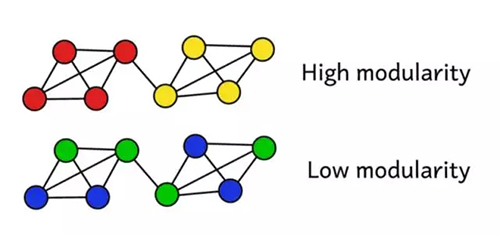
　　模塊性(modularity)是用于測量分區的「質量」的一種標準

模塊性可以使用以下公式進行計算：

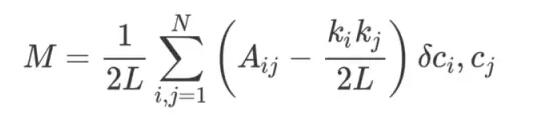
　　這個公式有點復雜，但我們分解它，讓我們可以更好地理解。

M 就是我們要計算的模塊性。

1/2L 告訴我們將后面的部分除以 2L，即網絡中邊的數量的兩倍。

Σ 符號表示求和，并且在該鄰接矩陣 A 中的每一行和列上進行迭代。如果你對這個符號不熟悉，可以將 i, j = 1 和 N 理解成編程語言中的 for-loop。在 Python 里面，可以寫成這樣：

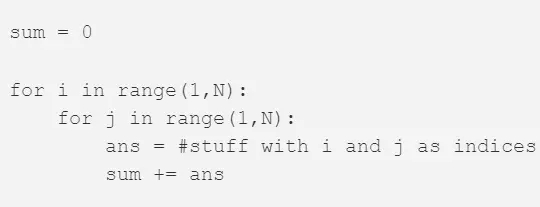
　　代碼里面的 #stuff with i and j(帶有 i 和 j 的那一坨)是什么?

括號中的內容表示從 A_ij 減去 ( k_i k_j ) / 2L。

A_ij 就是指該鄰接矩陣中第 i 行、第 j 列的值。

k_i 和 k_j 是指每個頂點的 degree——可以通過將每一行和每一列的項加起來而得到。兩者相乘再除以 2L 表示當該網絡是隨機分配的時候頂點 i 和 j 之間的預期邊數。

整體而言，括號中的項表示了該網絡的真實結構和隨機組合時的預期結構之間的差。研究它的值可以發現，當 A_ij = 1 且 ( k_i k_j ) / 2L 很小時，其返回的值最高。這意味著，當在定點 i 和 j 之間存在一個「非預期」的邊時，得到的值更高。

最后，我們再將括號中的項和 δc_i, c_j 相乘。δc_i, c_j 就是大名鼎鼎但基本無害的克羅內克 δ 函數(Kronecker-delta function)。下面是其 Python 解釋：

是的，就是那么簡單。克羅內克 δ 函數與兩個參數，如何這兩個參數相等則返回 1，如何不等，則返回 0.

也就是說，如果頂點 i 和 j 已經被放進了同一個聚類，那么δc_i, c_j = 1;否則它們不在同一個聚類，函數返回 0.

當我們將括號中的項與克羅內克 δ 函數相乘時，我們發現對于嵌套求和 Σ，當有大量「意外的(unexpected)」連接頂點的邊被分配給同一個聚類時，其結果是最高的。因此，模塊性是一種用于衡量將圖聚類成不同的團體的程度的方法。

除以 2L 將模塊性的上限值設置成了 1。模塊性接近或小于 0 表示該網絡的當前聚類沒有用處。模塊性越高，該網絡聚類成不同團體的程度就越好。通過是模塊性最大化，我們可以找到聚類該網絡的最佳方法。

注意我們必須預定義圖的聚類方式，才能找到評估一個聚類有多好的方法。不幸的是，使用暴力計算的方式來嘗試各種可能以尋找最高模塊性分數的聚類方式需要大量計算，即使在一個有限大小的樣本上也是不可能的。

組合學(combinatorics)告訴我們對于一個僅有 8 個頂點的網絡，就存在 4140 種不同的聚類方式。16 個頂點的網絡的聚類方式將超過 100 億種。32 個頂點的網絡的可能聚類方式更是將超過 128 septillion(10^21)種;如果你的網絡有 80 個頂點，那么其可聚類的方式的數量就已經超過了可觀測宇宙中的原子數量。

因此，我們必須求助于一種啟發式的方法，該方法在評估可以產生最高模塊性分數的聚類上效果良好，而且并不需要嘗試每一種可能性。這是一種被稱為 Fast-Greedy Modularity-Maximization(快速貪婪模塊性最大化)的算法，這種算法在一定程度上類似于上面描述的 agglomerative hierarchical clustering algorithm(集聚層次聚類算法)。只是 Mod-Max 并不根據距離(distance)來融合團體，而是根據模塊性的改變來對團體進行融合。

下面是其工作方式：

首先初始分配每個頂點到其自己的團體，然后計算整個網絡的模塊性 M。

第 1 步要求每個團體對(community pair)至少被一條單邊鏈接，如果有兩個團體融合到了一起，該算法就計算由此造成的模塊性改變 ΔM。

第 2 步是取 ΔM 出現了最大增長的團體對，然后融合。然后為這個聚類計算新的模塊性 M，并記錄下來。

重復第 1 步和 第 2 步——每一次都融合團體對，這樣最后得到 ΔM 的最大增益，然后記錄新的聚類模式及其相應的模塊性分數 M。

當所有的頂點都被分組成了一個巨型聚類時，就可以停止了。然后該算法會檢查這個過程中的記錄，然后找到其中返回了最高 M 值的聚類模式。這就是返回的團體結構。

4. 更多細節：

哇!這個過程真是有太多計算了，至少對我們人類而言是這樣。圖論中存在很多計算難題，常常是 NP-hard 問題——但其也在為復雜系統和數據集提供有價值的見解上具有出色的潛力。Larry Page 就知道這一點，其著名的 PageRank 算法就是完全基于圖論的——該算法在幫助谷歌在不到十年之內從創業公司成長為近乎世界主宰的過程中立下了汗馬功勞。

團體檢測(community detection)是現在圖論中一個熱門的研究領域，也存在很多可替代 Modularity-Maximization(盡管很有用，但也有缺點)的方法。

首先，它的聚集方式從指定尺寸的小團體開始，逐漸轉向越來越大的。這被稱為分辨率極限(resolution limit)——該算法不會搜索特定尺寸以下的團體。另一個挑戰則是超越一個顯著波峰的表現，Mod-Max 方法趨向于制造一個由很多高模塊化分數組成的「高原」，這有時會導致難以確定最大分數。

其他算法使用不同的方式來確定團體。Edge-Betweenness 是一個分裂算法，把所有頂點聚合到一個大集群中。它會持續迭代去除網絡中「最不重要」的邊緣數據，直到所有頂點都被分開為止。這一過程產生了層級結構，其中類似的頂點在結構中互相靠近。

另一種算法是 Clique Percolation，它考慮了圖團體之間可能的重疊。而另外一些算法基于圖中的隨機游動，還有譜聚類(spectral clustering)算法：從鄰接矩陣及派生矩陣的特征分解開始。這些方法被應用于特征提取任務，如計算機視覺。

給出每個算法的深入應用實例超出了本介紹的探究范圍。從數據中提取可用信息的有效方法在數十年前還是難以觸及的事物，但現在已經成為了非常活躍的研究領域。

四、結論

希望本文能對你有所啟發，讓你更好地理解機器如何了解大數據。未來是高速變革的，其中的許多變化將會由下一代或兩代中有能力的技術所驅動。

就像導語提到的，機器學習是一個非常有前景的研究領域，其中有大量復雜的問題需要以準確、有效的方式解決。對人類來說輕而易舉的任務在由機器完成的時候就需要創新性的解決方案。

在此領域中，我們仍有大量的任務需要完成，無論誰為下一個重大突破貢獻力量，無疑都會得到慷慨的回報。或許正在閱讀這篇文章的某個人就會成為下一個強大的算法發明者?所有偉大想法都是從零開始的。

原文：

https://medium.freecodecamp.com/how-machines-make-sense-of-big-data-an-introduction-to-clustering-algorithms-4bd97d4fbaba

【本文是51CTO專欄機構機器之心的原創譯文，微信公眾號“機器之心( id: almosthuman2014)”】