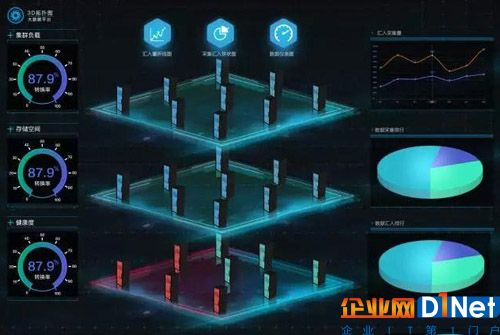
大數(shù)據(jù)時代下的今天,數(shù)據(jù)井噴似的增長,分析人員將這些龐大的數(shù)據(jù)匯總并進行分析,而分析出的成果如果是密密麻麻的文字,相信沒有幾個人能耐心看下去,所以我們就需要將數(shù)據(jù)可視化,所謂有圖有真相,用圖表甚至動態(tài)圖的形式將數(shù)據(jù)更加直觀的展現(xiàn)給用戶,減少用戶的閱讀和思考時間,以便很好地做出決策。
接下來本文就從幾個方面去講解數(shù)據(jù)可視化的一些技巧,順便帶大家領略一下可視化的風采。
數(shù)據(jù)可視化1:錯綜復雜散點圖
散點圖,在圖表界有萬表之王的稱號。
美國權威心理學專刊《Journal of the History of the Behavioral Sciences》(評價散點圖:“most versatile, polymorphic, and generally useful invention in the history of statistical graphics”這是信息圖表史上功能最多,形式多樣,應用范圍極為廣闊的一個偉大發(fā)明!
散點圖能獲此評價,絕對不是吹出來的。正如它的名字一樣,散點圖,可以一堆紛亂如麻,看似無跡可尋的數(shù)據(jù)顯示出內(nèi)在的關系邏輯來。散點圖已經(jīng)不僅僅是一個圖表了,它已經(jīng)演化為一個強大的分析工具,可以這么說,散點圖,就是為大數(shù)據(jù)而生的!
1.散點圖的前世今生
散點圖,是繪制在X軸和Y軸坐標系中,可以同時表述兩個變量的一組數(shù)據(jù)點。這些大量的數(shù)據(jù)點組合在一起,形成了一些形狀,揭示了數(shù)據(jù)背后的相關信息。散點圖溯源,散點圖的出現(xiàn)如同它的名字一樣,散亂不堪,無法理出一個有序的線索出來。
其實,對于散點數(shù)據(jù)的的視覺化應用,由來已久。好幾百年以來,人們一直將這些點放置在地圖,或者笛卡爾坐標系中。后來人們逐漸意識到,當這些數(shù)據(jù)以不同參數(shù),放置在直角坐標系中,很多不為人知的故事會偷偷地浮現(xiàn)出來。于是,散點圖逐漸開始流傳開來。散點圖,是廣大數(shù)據(jù)民工在長期的生產(chǎn)實踐中,通過不斷的探索和研究,最終發(fā)明出來的。散點圖從一開始的默默無聞,到最后轟動科學界,直到最后加冕圖表之王,其實也就是百十年的事。但是通過散點圖帶來的很多偉大的發(fā)現(xiàn),則徹底改變了我們的世界觀,推動了科學的發(fā)展。
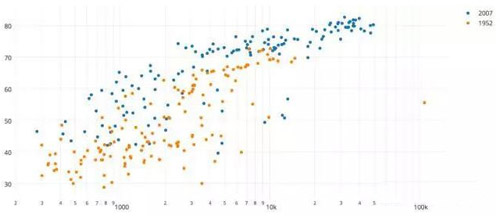

數(shù)據(jù)可視化2:似曾相識面積圖
面積圖正如我們平時所看到的大山那樣,斗轉(zhuǎn)星移滄海桑田,山依然是山。看上去樣子都差不多,但是仔細讀來,卻又內(nèi)藏玄機。面積圖也是一種隨著時間變化的圖表,而且很穩(wěn)重。無論你是要梳理出每個月各部門的凈收益,或者想看看從上世紀50年代以來各個音樂流派的普及流行程度,相信我,在那些與時間相關的圖表中,沒有什么比面積圖都可以更滿足你的需求了。下面就讓我們來好好認識一下這個似曾相識的面積圖吧!
1.了解面積圖
面積圖描繪了時間序列的關系,不過與線型圖不同,它還可以很直觀地表示面積大小的不同。
信息被標示在兩個軸之間,通過線段將數(shù)據(jù)點連綴起來,到這里為止,似乎和折線圖沒有什么不同。但是一旦我們將這條折線和軸之間的區(qū)域涂上顏色的話,意義就不一樣了。一般面積圖用與對兩種或者兩種以上的類別進行比較。
2.面積圖溯源
威廉.普萊菲爾——信息圖表的鼻祖!
就是他,發(fā)明了餅圖、條狀圖以及,沒錯,還有馬上要說的面積圖!
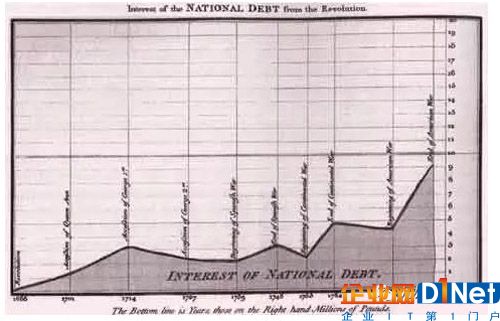
1786年,商業(yè)與政治圖表 史上第一張面積圖
3.面積圖的使用
關注大數(shù)據(jù)觀察網(wǎng)(微信公眾號:shuju_net)了解更多精彩資訊
面積圖是用來表述多類別整體運行趨勢的完美之選,所以不要試圖用它來展示單一的值。我們也常常用堆積面積圖來展示多類別中部分與整體的關系,或者同系列累計的值。面積圖有三種不同的形態(tài),根據(jù)數(shù)據(jù)以及背景的不同,均有其最佳的展示環(huán)境。
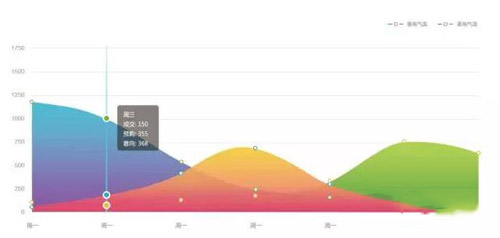
數(shù)據(jù)可視化3:絢麗多彩矩陣圖
矩陣圖就是從多維問題的事件中,找出成對的因素,排列成矩陣圖,然后根據(jù)矩陣圖來分析問題,確定關鍵點的方法,它是一種通過多因素綜合思考,探索問題的好方法從問題事項中,找出成對的因素群,分別排列成行和列,找出其間行與列的相關性或相關程度的大小的一種方法。
1.了解矩陣圖
在目的或結(jié)果都有二個以上,而要找出原因或?qū)Σ邥r,用矩陣圖比其他圖方便。
矩陣圖著眼于由屬于行的要素與屬于列的要素所構成之二元素的交點:
1.從二元的分配中探索問題的所在及問題的型態(tài)。
2.從元的關系中探求解決問題的構想。
在行與列的展開要素中,要尋求交叉點時,如果能夠取得數(shù)據(jù),就應依定量方式求出;如果無法取得數(shù)據(jù)時,則應依經(jīng)驗轉(zhuǎn)換成資訊,再決定之,所以決策交叉點時,以全員討論方式為之,并能在矩陣圖旁注上討論的成員、時間、地點及數(shù)據(jù)取得方式等簡歷,以便使用參考。
有時候交叉點的重要度各不相同,因此可用各種記號區(qū)別之。
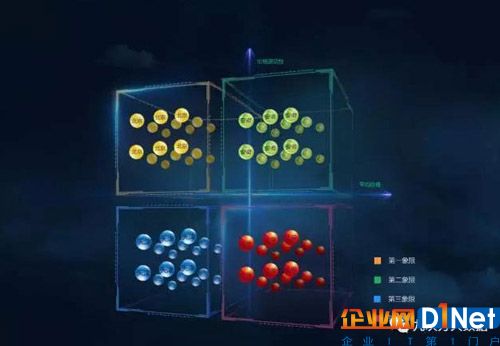

數(shù)據(jù)可視化4:神秘拓撲圖
拓撲結(jié)構圖是指由網(wǎng)絡節(jié)點設備和通信介質(zhì)構成的網(wǎng)絡結(jié)構圖。 在選擇拓撲結(jié)構時,主要考慮的因素有:安裝的相對難易程度、重新配置的難易程度、維護的相對難易程度、通信介質(zhì)發(fā)生故障時,受到影響的設備的情況。
































































































 京公網(wǎng)安備 11010502049343號
京公網(wǎng)安備 11010502049343號